A future topic will be the other types of math behind the machine learning; however, I will just be talking about linear algebra in this post.

From a high-level perspective, machine learning allows programs to learn from data to make predictions or decisions without being explicitly programmed.

Linear algebra is the foundation of many ML algorithms, it deals with vectors, matrices and their operations (very important).

• Vectors: Represent data points or feature sets.

• Matrices: Used for transformations and storing datasets.

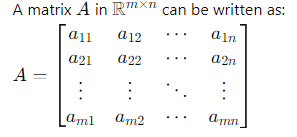
• Operations: Matrix multiplication, inversion, eigenvalues, and eigenvectors are crucial for algorithms like PCA (Principal Component Analysis) and neural networks.

For a square matrix A, the eigenvalue equation is Av=λvA where λ is an eigenvalue and v is the corresponding eigenvector.

This is where

• A is an n×n matrix.
• v is a non-zero vector in an eigenvector.
• λ is a scalar (an eigenvalue).

The equation Av=λv indicates that when the matrix A acts on the vector v it only stretches or shrinks v by a factor of λ and does not change its direction.

Finding Eigenvalues and Eigenvectors

To find the eigenvalues and eigenvectors of a matrix A, we follow these steps:

1. Eigenvalue Equation

Start with the equation: Av=λv

Rearrange to: (A−λI)v=0 where I is the identity matrix of the same dimension as A.

2. Determinant Condition

For non-trivial solutions (non-zero v), the matrix (A−λI) must be singular, meaning its determinant is zero: det(A−λI)=0

This equation is called the characteristic equation of the matrix A. Solving this polynomial equation in λ (typically of degree n for an n×n matrix) yields the eigenvalues λ1,λ2,…,λn.

The determinant is a scalar value that can be computed from the elements of a square matrix and provides important properties about the matrix. It is a useful tool in linear algebra for understanding the characteristics of a matrix, such as whether it is invertible and the volume scaling factor of the linear transformation it represents.

1. Determinant of a 2x2 Matrix

2. Determinant of a 3x3 Matrix

3. Determinant of an n×n Matrix

Properties of the Determinant

3. Solving for Eigenvectors

Once the eigenvalues λ are found, substitute each λ back into the equation: (A−λI)v=0

This equation forms a system of linear equations. Solve this system to find the eigenvectors v corresponding to each eigenvalue λ.

Example

Let’s consider a simple 2×2 matrix A:

Step 1: Find the Characteristic Equation

Step 2: Solve for Eigenvectors

Vector Spaces

A vector space is a set of vectors, along with operations of vector addition and scalar multiplication, that satisfies certain axioms (such as associativity, distributivity, and the existence of an additive identity and additive inverses).

Basis and Dimension

• Basis: A basis of a vector space is a set of vectors that are linearly independent and span the space. Every vector in the space can be uniquely expressed as a linear combination of the basis vectors.
• Dimension: The dimension of a vector space is the number of vectors in a basis for the space.

Orthogonality

Two vectors are orthogonal if their dot product is zero. Orthogonality is a key concept in many applications, including the decomposition of spaces and the Gram-Schmidt process for orthogonalizing a set of vectors.

Applications in Machine Learning

• Data Representation: Data is often represented as vectors (data points) and matrices (datasets).
• Model Parameters: Parameters in linear models (like weights in regression) are vectors.
• Dimensionality Reduction: Techniques like PCA use eigenvectors and eigenvalues to reduce the dimensionality of data.
• Optimization: Gradient descent involves operations on vectors and matrices.
• Neural Networks: Operations in neural networks (forward pass, backpropagation) are fundamentally linear algebra operations.